
Felix KälbererI am a former member of the Mathematical Geometry Processing Group headed by Konrad Polthier. |

|
|
Projects |
||||

Hierarchical parameterization of arbitrary meshes |
Surface meshes often appear in a quality and resolution which is unsuitable for many geometry processing algorithms. This project aims at the automatic improvement of surface meshes.
Funding by mental images GmbH (Jan 2006 - Jan 2010) |
|||
|
Project F6 - Multilevel Methods on Manifold Meshes (04/2005 - 03/2010) This project addresses the strong needs for multilevel algorithms in industrial applications and in computer graphics where large surface meshes must be efficiently processed. Typical applications are solutions of PDEs on surfaces, surface optimization, and automatic mesh parametrization. I am associate member to this DFG Research Center Matheon project (Feb 2004 - Dec 2007) |
||||
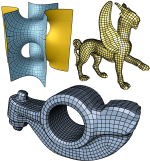
Mesh Compression |
Numerical simulations and the rendering of complex virtual scenes is often limited by the huge size of the involved geometry meshes. This project researches the geometric and topological properties of mesh representations to solve the following challenges:
We develop algorithms and implementations for mesh compression, including surface attributes like textures and normals. Puplication: FreeLence - Coding with free Valences. (with Konrad Polthier, Ulrich Reitebuch, and Max Wardetzky), Eurographics 2005 My work was supported by DFG Research Center Matheon in cooperation with mental images GmbH (Apr 2004 - Mar 2005) |
|||
|
|
|||

PhD Thesis |
PhD Thesis: Low Distortion Surface Parameterization, 2013.
This work presents new algorithms for high quality surface parameterization, that is, generation of a mapping between a surface and the Euclidean plane. Through this correspondence, the existing structure of the plane is transferable onto the surface.
|
|||
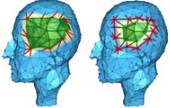
Hierarchy Coding |
Felix Kälberer, Konrad Polthier, and Christoph von Tycowicz: Context-Based Coding of Adaptive Multiresolution Meshes, Computer Graphics Forum, to appear. Multiresolution meshes provide an efficient and structured representation of geometric objects. To increase the mesh resolution only at vital parts of the object, adaptive refinement is widely used. We propose a lossless compression scheme for these adaptive structures that exploits the parent-child relationships inherent to the mesh hierarchy. We use the rules that correspond to the adaptive refinement scheme and store bits only where some freedom of choice is left, leading to compact codes that are free of redundancy. Moreover, we extend the coder to sequences of meshes with varying refinement. The connectivity compression ratio of our method exceeds that of state-of-the-art coders by a factor of 2 to 7. For efficient compression of vertex positions we adapt popular wavelet-based coding schemes to the adaptive triangular and quadrangular cases to demonstrate the compatibility with our method. Akin to state-of-the-art coders, we use a zerotree to encode the resulting coefficients. Using improved context modeling we enhanced the zerotree compression, cutting the overall geometry data rate by 7% below those of the successful Progressive Geometry Compression. More importantly, by exploiting the existing refinement structure we achieve compression factors that are 4 times greater than those of coders which can handle irregular meshes. |
|||

Stripe Parameterization |
Felix Kälberer, Matthias Nieser, and Konrad Polthier: Stripe Parameterization of Tubular Surfaces. Topological Data Analysis and Visualization: Theory, Algorithms and Applications, V. Pascucci and H. Hagen and J. Tierny and X. Tricoche (eds.), Springer, 2011 We present a novel algorithm for automatic parameterization of tube-like surfaces of arbitrary genus such as the surfaces of knots, trees, blood vessels, neurons, or any tubular graph with a globally consistent stripe texture. We use the principal curvature frame field of the underlying tube-like surface to guide the creation of a global, topologically consistent stripe parameterization of the surface. Our algorithm extends the QuadCover algorithm and is based, first, on the use of so-called projective vector fields instead of frame fields, and second, on different types of branch points. That does not only simplify the mathematical theory, but also reduces computation time by the decomposition of the underlying stiffness matrices. |
|||
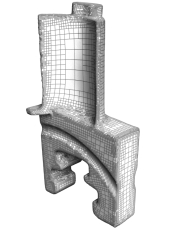
Hierarchy Compression |
Felix Kälberer, Konrad Polthier, and Christoph von Tycowicz: Lossless Compression of Adaptive Multiresolution Meshes, Sibgrapi 2009 Technical Paper. We present a novel coder for lossless compression of adaptive multiresolution meshes that exploits their special hierarchical structure. The heart of our method is a new progressive connectivity coder that can be combined with leading geometry encoding techniques. The compressor uses the parent/child relationships inherent to the hierarchical mesh. We use the rules that accord to the refinement scheme and store bits only where it leaves freedom of choice, leading to compact codes that are free of redundancy. To illustrate our scheme we chose the widespread red-green refinement, but the underlying concepts can be directly transferred to other adaptive refinement schemes as well. The compression ratio of our method exceeds that of state-of-the-art coders by a factor of 2 to 3 on most of our benchmark models. |
|||
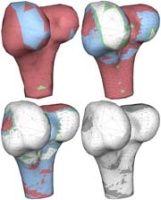
Surface Parameterization |
Felix Kälberer, Matthias Nieser, and Konrad Polthier: QuadCover - Surface Parameterization using Branched Coverings. Computer Graphics Forum, Eurographics 2007. We introduce an algorithm for automatic computation of global parameterizations on arbitrary simplicial 2-manifolds whose parameter lines are guided by a given frame field, for example by principal curvature frames. The parameter lines are globally continuous, and allow a remeshing of the surface into quadrilaterals. The algorithm converts a given frame field into a single vector field on a branched covering of the 2-manifold, and generates an integrable vector field by a Hodge decomposition on the covering space. Except for an optional smoothing and alignment of the initial frame field, the algorithm is fully automatic and generates high quality quadrilateral meshes. |
|||
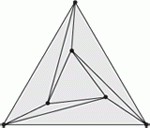
Discrete Laplace Operators |
Max Wardetzky,
Saurabh Mathur,
Felix Kälberer, and
Eitan Grinspun:
Discrete Laplace operators: No free lunch.
Symposium on Geometry Processing, 2007.
Discrete Laplace operators are ubiquitous in applications spanning geometric modeling to simulation. For robustness and efficiency, many applications require discrete operators that retain key structural properties inherent to the continuous setting. Building on the smooth setting, we present a set of natural properties for discrete Laplace operators for triangular surface meshes. We prove an important theoretical limitation: discrete Laplacians cannot satisfy all natural properties; retroactively, this explains the diversity of existing discrete Laplace operators. Finally, we present a family of operators that includes and extends well-known and widely-used operators. |
|||
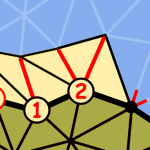
Mesh Compression |
Felix Kälberer,
Konrad Polthier,
Ulrich Reitebuch, and
Max Wardetzky:
FreeLence - Coding with Free Valences.
Eurographics 2005.
We introduce FreeLence, a novel and simple compression coder for triangle meshes. Our method uses free valences and exploits geometric information for connectivity encoding. Furthermore, we introduce a novel linear prediction scheme for geometry compression of 3D meshes. Together, these approaches yield a significant entropy reduction for mesh encoding with an average of 20-30% over leading region-growing coders, both for connectivity and geometry. |
|||
|
|
|||
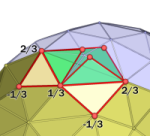
Mesh Compression |
Geometry and Connectivity Compression of
Triangle Meshes.
Diploma Thesis, 2005.
|
|||
|
|
|||
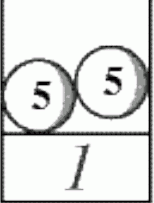
Krawattenrätsel |
In summer 2008, the German Mathematical Society (DMV) and Spektrum Akademischer Verlag offered a 1,000 Euro award for the solution of the following Krawattenrätsel (Sorting Pairs in Bins) that appeared in Peter Winkler's wonderful book Mathematical Puzzles:
The solution of the Krawattenrätsel (English version) with Matthias Nieser and Ulrich Reitebuch improved the known upper bound for the number of steps and won a 1st prize of 400 Euros. |
|||



